问题说明

这个世界是三维的，也就是说要用坐标 $(x, y, z)$ 和三个数来表示位置。这次我们考虑的是一个更高维度的 $200$ 维世界。也就是说，一个点的坐标由 $(x_1, x_2, ..., x_{200})$ 和 $200$ 个数表示。

现在，在 $200$ 维空间上有 $5,000$ 个不同编号从 $1$ 到 $5,000$ 的点。对于这 $5,000$ 个点，我们考虑连接点之间满足以下条件的方法：

• 任意两个点之间都可以通过移动到相连的点来到达。
• 移动过程中不能经过同一个点超过两次，这样移动方法就唯一确定了。

换句话说，我们希望将这些点连接成一棵树。

然后，作为竞赛题目的约定，我们考虑尽量将连接成本降低。在这里，连接点 $(a_1, a_2, ..., a_{200})$ 和 $(b_1, b_2, ..., b_{200})$ 的成本定义如下：

• 两个点的 相似度 可以通过以下公式确定。（这被称为 "余弦相似度"）
  
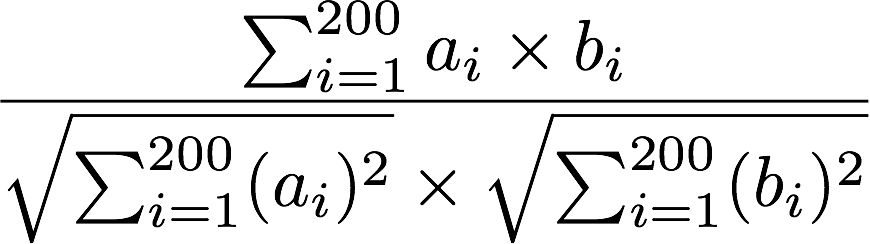
• 在这种情况下，连接两个点的成本为 $1 - \text{相似度}$。也就是说，相似度越高，成本越低，相似度越低，成本越高。

整体成本由连接点所需的成本总和决定。在这种情况下，请编写一个程序来寻找尽量降低成本的方法。但是，并不需要将成本最小化，如果输出的连接方式的成本在 最小成本的 $1.01$ 倍以内，则视为通过。

输入格式

输入以以下格式从标准输入中给出。

$seed$

• 第 $1$ 行包含一个整数 $seed (1 ≦ seed ≦ 10^6)$。

实际点的坐标由使用 $seed$ 的伪随机数生成。所有点的坐标值在 $-50,000$ 到 $50,000$ 之间，并且不能为零的整数中均匀选择。具体来说，可以通过以下伪代码确定坐标的值。

x = 123456789
y = 362436069
z = 521288629
w = seed

for i = 1 to 5000
  for j = 1 to 200
    t = x ^ (x << 11)
    x = y
    y = z
    z = w
    w = (w ^ (w >> 19)) ^ (t ^ (t >> 8))

    v = w % 100000 - 50000
    if v >= 0 then
      v = v + 1

    (i 番目の点の座標の j 番目の値) = v

这里的 seed 是输入中的 $seed$ 的值。

变量 x, y, z, w, t 是 $32$ 位无符号整数型，使用 = 进行赋值，使用 ^ 进行按位异或操作，使用 << 进行向左移位操作，使用 >> 进行向右移位操作。

输出格式

请输出恰好 $4,999$ 行。每行包含两个整数 $p$, $q$，表示点 $p$ 和点 $q$ 之间的连接。

输出末尾需包含换行。

示例输入1

1

示例输出1

输出较大，不予显示，但该用例的最小成本约为 $3739.378294998$。

示例输入2

2

示例输出2

该用例的最小成本约为 $3741.147062644$。