问题描述

有$N(N+1)/2$个点排列成一个等边三角形，其中每边包含$N$个点，如下所示。从上往下第$i$行从左往右第$j$个点表示为$(i, j)$（$1 \leq i \leq N$, $1 \leq j \leq i$）。此外，我们将$(i+1, j)$称为$(i, j)$的左下方的点，将$(i+1, j+1)$称为$(i, j)$的右下方的点。

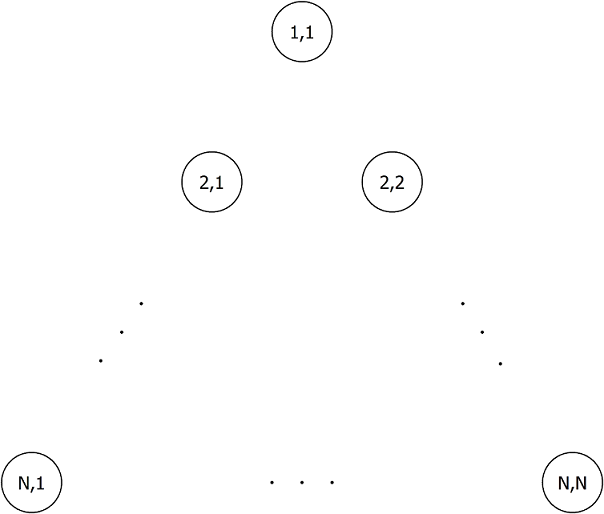
高桥通过连接这些点绘制了$M$条多边形线段$L_1, L_2, ..., L_M$。每条$L_i$从$(1, 1)$开始，并访问当前点的左下方或右下方的点$N-1$次。更准确地说，存在$X_{i,1}, ..., X_{i,N}$使得：

• $L_i$按照顺序连接$N$个点$(1, X_{i,1}), (2, X_{i,2}), ..., (N, X_{i,N})$。
• 对于每个$j=1, 2, ..., N-1$，要么$X_{i,j+1} = X_{i,j}$，要么$X_{i,j+1} = X_{i,j}+1$。

高桥希望绘制这些线段，使得$L_{i+1}$的任何部分都不在$L_i$的左边。也就是说，对于每个$j=1, 2, ..., N$，必须满足$X_{1,j} \leq X_{2,j} \leq ... \leq X_{M,j}$。

此外，对线段的形状有$K$个约束条件必须遵循。第$i$个条件表示为$(A_i, B_i, C_i)$，其中：

• 如果$C_i=0$，则$L_{A_i}$必须在第$B_i$步访问左下方的点。
• 如果$C_i=1$，则$L_{A_i}$必须在第$B_i$步访问右下方的点。

也就是说，必须满足$X_{A_i, {B_i}+1} = X_{A_i, B_i} + C_i$。

高桥有多少种方式可以绘制$M$条多边形线段？找到模$1000000007$的计数。

注意事项

在提交之前，强烈建议使用"自定义测试"来测量代码的执行时间。

约束条件

• $1 \leq N \leq 20$
• $1 \leq M \leq 20$
• $0 \leq K \leq (N-1)M$
• $1 \leq A_i \leq M$
• $1 \leq B_i \leq N-1$
• $C_i = 0$ 或者 $1$
• $(A_i, B_i)$不会出现两次。

---

输入

输入以以下格式从标准输入给出：

$N$ $M$ $K$ $A_1$ $B_1$ $C_1$ $A_2$ $B_2$ $C_2$ : $A_K$ $B_K$ $C_K$

输出

输出高桥绘制$M$条多边形线段的方法数，对$1000000007$取模。

---

示例输入1

3 2 1
1 2 0

示例输出1

6

有六种绘制线段的方法，如下所示。其中，红线代表$L_1$，绿线代表$L_2$。

---

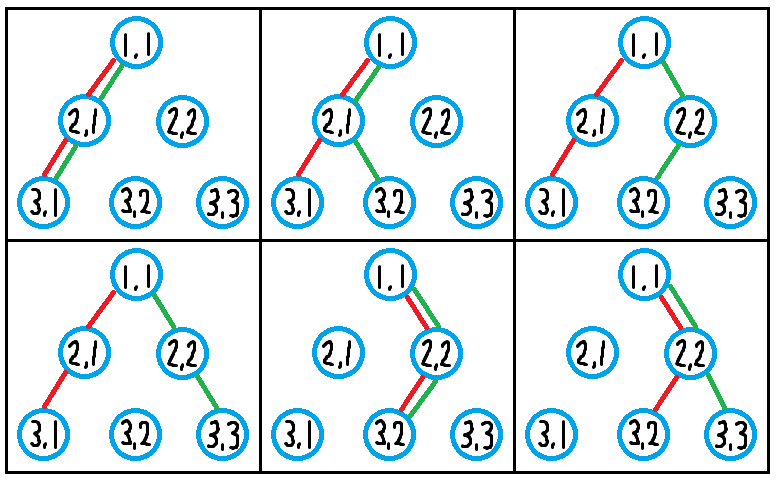
示例输入2

3 2 2
1 1 1
2 1 0

示例输出2

0

---

示例输入3

5 4 2
1 3 1
4 2 0

示例输出3

172

---

示例输入4

20 20 0

示例输出4

881396682