题目描述

Nuske有一个由 $N$ 行 $M$ 列的正方形格子网格。行从上到下编号为 $1$ 到 $N$，列从左到右编号为 $1$ 到 $M$。网格中的每个格子要么是蓝色要么是白色。如果 $S_{i,j}$ 是 $1$，表示第 $i$ 行第 $j$ 列的格子是蓝色；如果 $S_{i,j}$ 是 $0$，表示该格子是白色。对于任意一对蓝色格子 $a$ 和 $b$，存在至多一条路径，该路径以 $a$ 为起点，依次经过相邻的（相邻边）蓝色格子，最终到达 $b$，且不能重复经过同一个格子。

Nuske的永恒对手Phantom Thnook向Nuske提出了 $Q$ 个查询。第 $i$ 个查询包含四个整数 $x_{i,1}$、$y_{i,1}$、$x_{i,2}$ 和 $y_{i,2}$，询问他以下问题：当将网格上以 $x_{i,1}$ 行、$x_{i,2}$ 行、$y_{i,1}$ 列和 $y_{i,2}$ 列为边界（包括边界）的矩形区域切割出来后，该区域内有多少个由蓝色格子组成的连通分量？

处理所有的查询。

约束条件

• $1 ≤ N,M ≤ 2000$
• $1 ≤ Q ≤ 200000$
• $S_{i,j}$ 要么是 $0$ 要么是 $1$。
• $S_{i,j}$ 满足题目中给出的条件。
• $1 ≤ x_{i,1} ≤ x_{i,2} ≤ N(1 ≤ i ≤ Q)$
• $1 ≤ y_{i,1} ≤ y_{i,2} ≤ M(1 ≤ i ≤ Q)$

输入

输入从标准输入读取，格式如下：

$N$ $M$ $Q$ $S_{1,1}$..$S_{1,M}$ : $S_{N,1}$..$S_{N,M}$ $x_{1,1}$ $y_{i,1}$ $x_{i,2}$ $y_{i,2}$ : $x_{Q,1}$ $y_{Q,1}$ $x_{Q,2}$ $y_{Q,2}$

输出

对于每个查询，打印区域内由蓝色格子组成的连通分量的数量。

示例输入 1

3 4 4
1101
0110
1101
1 1 3 4
1 1 3 1
2 2 3 4
1 2 2 4

示例输出 1

3
2
2
2

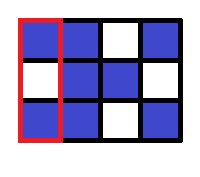
在第一个查询中，指定了整个网格。有三个由蓝色格子组成的连通分量，所以应该打印 $3$。

在第二个查询中，指定了红色框中的区域。有两个由蓝色格子组成的连通分量，所以应该打印 $2$。注意，原始网格中属于同一连通分量的方格可能属于不同的连通分量。

示例输入 2

5 5 6
11010
01110
10101
11101
01010
1 1 5 5
1 2 4 5
2 3 3 4
3 3 3 3
3 1 3 5
1 1 3 4

示例输出 2

3
2
1
1
3
2