问题陈述

高桥王国有一条铁路。铁路由 $N$ 节段组成，编号为 $1$、$2$、...、$N$，以及 $N+1$ 个车站，编号为 $0$、$1$、...、$N$。第 $i$ 节段直接连接车站 $i-1$ 和 $i$。列车通过第 $i$ 节段的时间为 $A_i$ 分钟，不论方向如何。$N$ 个节段中的每个节段要么是整个长度单线轨道，要么是整个长度双线轨道。如果 $B_i = 1$，则表示第 $i$ 节段是单线轨道；如果 $B_i = 2$，则表示第 $i$ 节段是双线轨道。双线轨道上的两列车可以交叉行驶，但在单线轨道上不能交叉行驶。列车也可以在车站交叉。

Snuke 正在制定该铁路的时刻表。在这个时刻表中，铁路上的列车每隔 $K$ 分钟行驶一次，如下图所示。这里，粗线表示在铁路上行驶的列车的位置。（请参见示例 1 进行说明。）

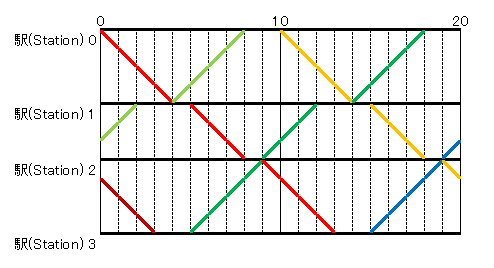
在制定这样的时刻表时，找到列车从 $0$ 号车站出发并到达 $N$ 号车站所需时间的最小总和，以及列车从 $N$ 号车站出发并到达 $0$ 号车站所需时间的总和。可以证明，如果存在满足本问题条件的时刻表，则这个最小总和始终是一个整数。

形式上，列车到达和离开的时间必须满足以下条件：

• 每个列车要么从 $0$ 号车站出发并前往 $N$ 号车站，或者从 $N$ 号车站出发并前往 $0$ 号车站。
• 每个列车需要花费恰好 $A_i$ 分钟通过第 $i$ 节段。例如，如果一列开往 $N$ 号车站的列车在时间 $t$ 从 $i-1$ 号车站出发，那么该列车将在恰好 $t+A_i$ 的时间到达 $i$ 号车站。
• 假设一辆开往 $N$ 号车站的列车在时间 $s$ 到达一个车站，并在时间 $t$ 离开该车站。那么下一辆开往 $N$ 号车站的列车将在时间 $s+K$ 到达该车站，并在时间 $t+K$ 离开该车站。此外，上一辆开往 $N$ 号车站的列车将在时间 $s-K$ 到达该车站，并在时间 $t-K$ 离开该车站。对于开往 $0$ 号车站的列车也是如此。
• 相反方向行驶的列车不能同时在同一条单线轨道上行驶（除了两端的车站）。

约束条件

• $1 \leq N \leq 100000$
• $1 \leq K \leq 10^9$
• $1 \leq A_i \leq 10^9$
• $A_i$ 是整数。
• $B_i$ 要么为 $1$，要么为 $2$。

得分说明

• 在价值为 $500$ 分的测试集中，所有节段都是单线轨道。即 $B_i = 1$。
• 在价值为另外 $500$ 分的测试集中，$N \leq 200$。

---

输入

输入以以下格式从标准输入给出：

$N$ $K$ $A_1$ $B_1$ $A_2$ $B_2$ : $A_N$ $B_N$

输出

输出一个整数，表示列车从 $0$ 号车站出发并到达 $N$ 号车站所需时间的最小总和，以及列车从 $N$ 号车站出发并到达 $0$ 号车站所需时间的总和。如果无法创建满足条件的时刻表，则输出 $-1$。

---

示例输入 1

3 10
4 1
3 1
4 1

示例输出 1

26

例如，在以下时刻表中，有一个问题的时间总和为 $26$ 分钟：

在该时刻表中，由红色线表示的列车在时间 $0$ 从 $0$ 号车站出发，到达 $1$ 号车站的时间为 $4$，在时间 $5$ 从 $1$ 号车站出发，到达 $2$ 号车站的时间为 $8$，以此类推。

---

示例输入 2

1 10
10 1

示例输出 2

-1

---

示例输入 3

6 4
1 1
1 1
1 1
1 1
1 1
1 1

示例输出 3

12

---

示例输入 4

20 987654321
129662684 2
162021979 1
458437539 1
319670097 2
202863355 1
112218745 1
348732033 1
323036578 1
382398703 1
55854389 1
283445191 1
151300613 1
693338042 2
191178308 2
386707193 1
204580036 1
335134457 1
122253639 1
824646518 2
902554792 2

示例输出 4

14829091348