问题描述

Sigma和Sugim正在玩一个游戏。

游戏在一个有$N$个顶点的图上进行，顶点编号为$1$到$N$。该图有$N-1$条红色边和$N-1$条蓝色边，每种颜色的边数为$N-1$，并且每种颜色的边构成一棵树。红色边由整数对$(a_i, b_i)$表示，蓝色边由整数对$(c_i, d_i)$表示。

每个玩家都有自己的棋子。最初，Sigma的棋子位于顶点$X$，Sugim的棋子位于顶点$Y$。

游戏按照回合进行，回合从第$1$回合开始编号。Sigma进行回合$1, 3, 5, ...$，Sugim进行回合$2, 4, 6, ...$。

在每个回合中，当前玩家要么移动他的棋子，要么不做任何操作。在这里，Sigma只能将他的棋子移动到与当前顶点直接相连的顶点上，通过一条红色边。同样地，Sugim只能将他的棋子移动到与当前顶点直接相连的顶点上，通过一条蓝色边。

当两个棋子来到同一个顶点时，游戏立即结束。如果游戏在第$i$回合的操作之后结束，则$i$是游戏中的总回合数。

Sigma的目标是使总回合数尽可能地大，而Sugim的目标是使总回合数尽可能地小。

假设两位玩家都以最优方式实现各自的目标，确定游戏是否会在有限的回合内结束。如果答案是肯定的，请找出游戏中的回合数。

约束条件

• $2 ≦ N ≦ 200,000$
• $1 ≦ X, Y ≦ N$
• $X \neq Y$
• $1 ≦ a_i, b_i, c_i, d_i ≦ N$
• 每种颜色（红色和蓝色）的$N-1$条边构成一棵树。

输入

输入以以下格式从标准输入中给出：

$N$ $X$ $Y$ $a_1$ $b_1$ $a_2$ $b_2$ $:$ $a_{N-1}$ $b_{N-1}$ $c_1$ $d_1$ $c_2$ $d_2$ $:$ $c_{N-1}$ $d_{N-1}$

输出

如果游戏将在有限次回合内结束，请输出回合数。否则，请输出-1。

样例输入 1

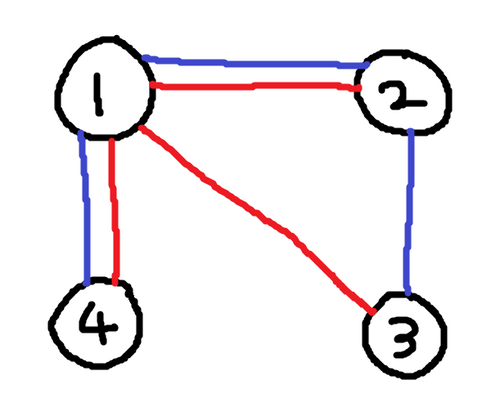
4 1 2
1 2
1 3
1 4
2 1
2 3
1 4

样例输出 1

4

样例输入 2

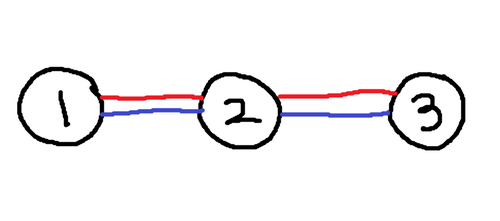
3 3 1
1 2
2 3
1 2
2 3

样例输出 2

4

样例输入 3

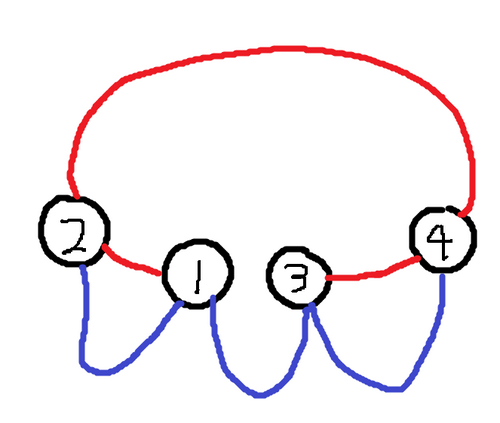
4 1 2
1 2
3 4
2 4
1 2
3 4
1 3

样例输出 3

2

样例输入 4

4 2 1
1 2
3 4
2 4
1 2
3 4
1 3

样例输出 4

-1

样例输入 5

5 1 2
1 2
1 3
1 4
4 5
2 1
1 3
1 5
5 4

样例输出 5

6