题目描述

给定一个无向无权图，其中包含 $N$ 个顶点和 $M$ 条边，图中既没有自环也没有重复边。
这里，自环 是一条满足 $a_i = b_i (1≤i≤M)$ 的边，而 重复边 是两条边满足 $(a_i,b_i)=(a_j,b_j)$ 或 $(a_i,b_i)=(b_j,a_j) (1≤i<j≤M)$。
有多少不同的路径从顶点 $1$ 开始并且恰好访问所有的顶点？
在这里，路径的端点也被认为是已访问的。

例如，假设给出了图 1 中所示的无向图。

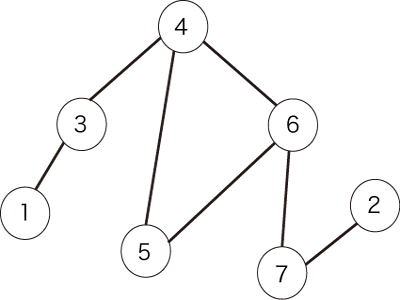
图 1：一个无向图的例子

图 2 中所示的路径满足这个条件。

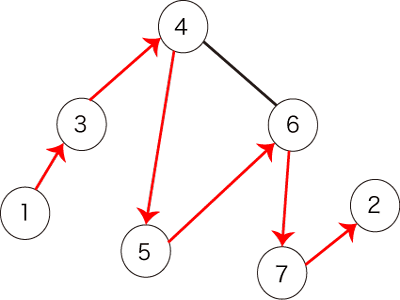
图 2：满足条件的一条路径的例子

然而，图 3 中所示的路径不满足这个条件，因为它没有访问到所有的顶点。

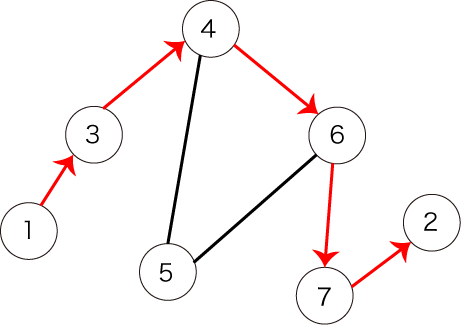
图 3：不满足条件的一条路径的例子

图 4 中所示的路径也不满足这个条件，因为它没有从顶点 $1$ 开始。

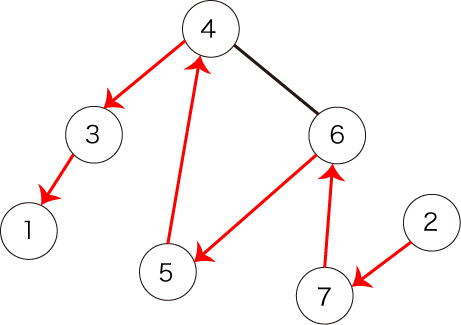
图 4：另一个不满足条件的一条路径的例子

约束条件

• $2≤N≤8$
• $0≤M≤N(N-1)/2$
• $1≦a_i<b_i≦N$
• 给定的图中既没有自环也没有重复边。

输入

输入以以下格式从标准输入中给出：

$N$ $M$
$a_1$ $b_1$
$a_2$ $b_2$ $:$
$a_M$ $b_M$

输出

输出从顶点 $1$ 开始并且恰好访问所有的顶点的不同路径数量。

示例输入 1

3 3
1 2
1 3
2 3

示例输出 1

2

给定的图如下所示：

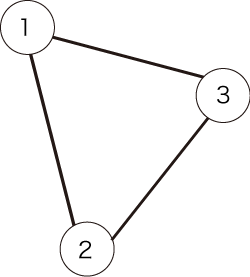
满足条件的两条路径如下：

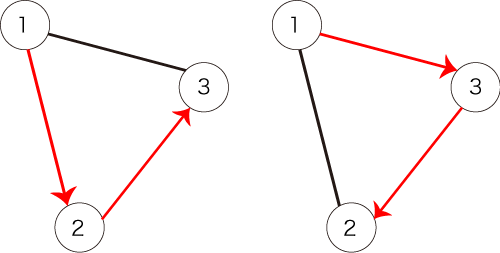
示例输入 2

7 7
1 3
2 7
3 4
4 5
4 6
5 6
6 7

示例输出 2

1

这个测试案例与题目描述中的相同。