问题描述

你和高桥君住在AtCoder王国。AtCoder王国有N个城镇和一些相互连接的道路，道路可以双向移动。这N个城镇分别称为城镇1，城镇2，...，城镇N。

高桥君决定去你家玩，并且他从城镇a出发，经过AtCoder王国的某个城镇，最终到达了你家所在的城镇b。

高桥君声称他是通过最短路径从城镇a到城镇b的，但你觉得他可能在撒谎。然而，由于你完全不知道哪些道路连接了哪些城镇，所以无法判断高桥君走过的路径是否真的是最短路径。

你成功地询问了高桥君经过城镇的顺序。然而，这个信息并不包括起点/终点城镇a和b。

根据这个信息，你打算编写一个程序来判断高桥君是否有可能是以最短路径移动的。最短路径从城镇a到城镇b是指在移动路径中，道路通行次数最少的路径。

如果存在一种城镇和道路的配置使得高桥君经过的路径是最短路径，则可以说他很可能是以最短路径移动的。另一方面，如果不存在这样的配置，则可以说他很可能不是以最短路径移动的。

---

输入

输入以以下形式从标准输入给出：

N a b K P1 P2 ... PK

• 第1行包含一个整数N（2≦N≦100），表示AtCoder王国中存在的城镇数量。
• 第2行包含两个整数a和b（1≦a,b≦N，a≠b），表示高桥君出发的城镇和你家所在的城镇的编号。
• 第3行包含一个整数K（1≦K≦100），表示高桥君在移动过程中经过的城镇数量。
• 第4行包含按顺序给出的高桥君经过的城镇编号。其中，第i个整数Pi（1≦Pi≦N）表示高桥君从城镇a出发后经过第i个城镇的编号。

相邻的元素$P_i$是不同的。换句话说，对于所有$2≤j≤K$，都成立$P_j≠P_{j-1}$。而且，$P_1 ≠ a$和$P_K ≠ b$都成立。

输出

输出一行，如果高桥君有可能是以最短路径移动的，则输出YES，否则输出NO。

记得输出一个换行符。

---

示例1

5
1 5
3
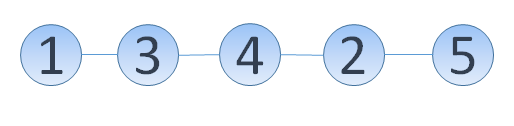
3 4 2

输出示例1

YES

例如，考虑以下道路配置：$1→3→4→2→5$，这条路径就是最短路径。

---

示例2

7
1 3
4
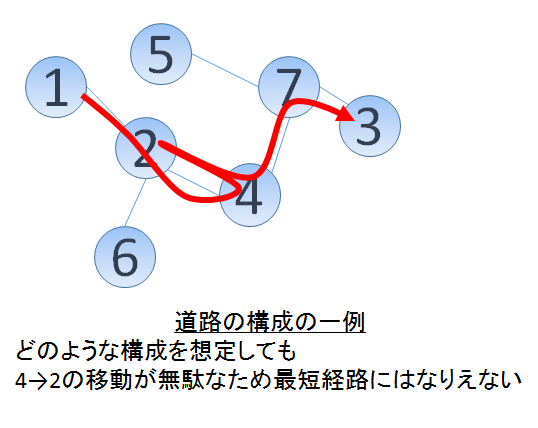
2 4 2 7

输出示例2

NO

不存在一种道路配置使得$1→2→4→2→7→3$成为最短路径。无论道路如何配置，都必然可以省略再次访问同一个城镇的移动。

---

示例3

4
1 4
3
2 1 3

输出示例3

NO

高桥君移动了$1→2→1→3→4$。尽管他返回了一次起点，但这样的移动方式无法实现最短路径。

---

示例4

4
1 4
3
2 4 3

输出示例4

NO

高桥君移动了$1→2→4→3→4$。即使他已经到达了终点，他仍然继续移动。

---

示例5

20
1 4
12
2 3 5 7 8 9 10 11 12 15 13 14

输出示例5

YES

---