问题文

高桥君喜欢迷宫。现在，他正在尝试解决一个由二维面板组成的迷宫，可以在上下左右移动。迷宫的布局如下：

• 首先，给出面板的大小和迷宫的起始点和目标点的坐标。
• 然后，给出面板上每个单元格是通行空地（.）还是不可通行的墙壁（#）。迷宫被墙壁包围。起点和终点都是空地，并且从起点到终点必定可达，即通过空地行走一定可以到达终点。具体来说，您可以参考输入输出示例。

现在，他想要找出解决上述迷宫所需的最小移动步数。他在研究如何求解时发现了一种称为“广度优先搜索”的方法。广度优先搜索的具体步骤如下：

• 从起点开始，按距离起点最近（即到达目标所需的最少步数）的单元格顺序确定到达目标的步数。以图1中的迷宫为例进行说明。

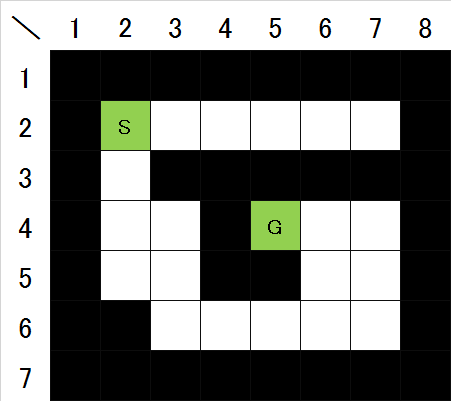
图1. 用于说明的面板

• 首先，起点到起点的距离为0（当然）, 所以将其设置为最短步数0（图2）。

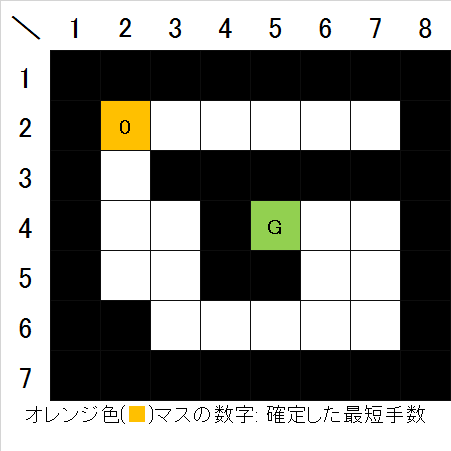
图2. 距离起点0的单元格确定(初始状态)

• 接下来，确定距离起点1步的起点周围的空地单元格（图3）。

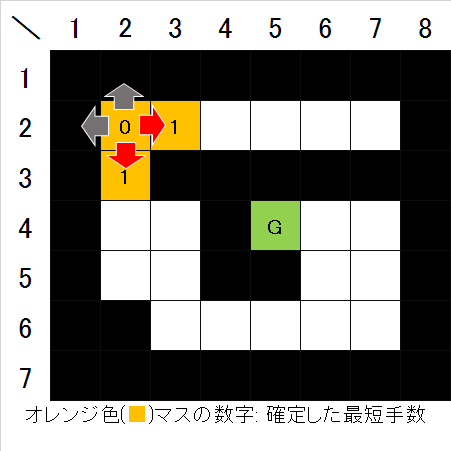
图3. 距离起点1的单元格确定

• 然后，检查已确定距离1的每个单元格的四邻域，如果仍有未确定的空地单元格，则将该单元格设置为步数2（图4）。

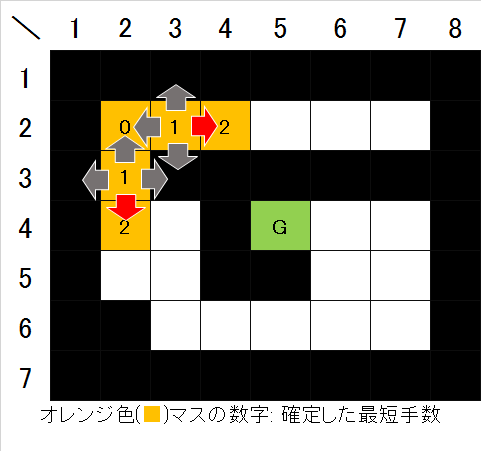
图4. 距离起点2的单元格确定

• 然后，检查已确定距离2的每个单元格的四邻域，如果仍有未确定的空地单元格，则将该单元格设置为步数3（图5）。

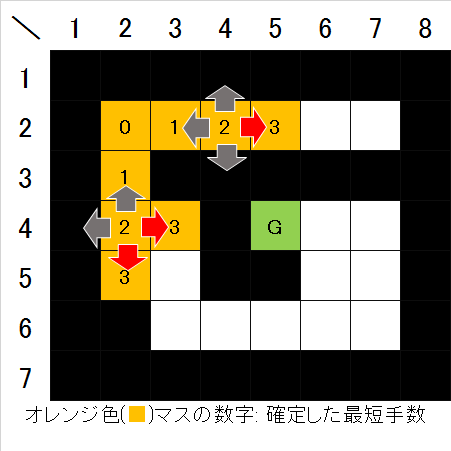
图5. 距离起点3的单元格确定

• 然后，检查已确定距离3的每个单元格的四邻域，如果仍有未确定的空地单元格，则将该单元格设置为步数4（图6）。

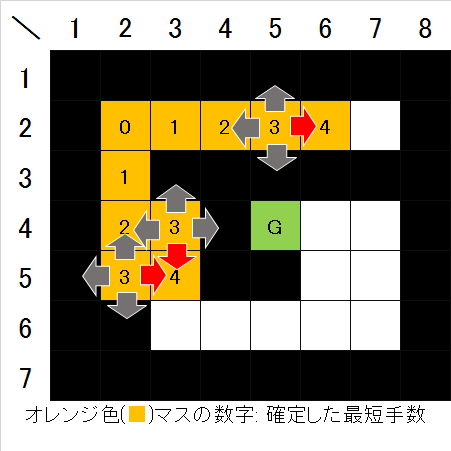
图6. 距离起点4的单元格确定

• 重复上述步骤，直到没有进一步的最短步数更新为止。这样，可以确定从起点可达的所有空地单元格的最短步数（图7）。由于起点和终点可以通过空地到达，因此也可以确定到达终点的最短步数。

图7. 所有可达单元格的最短步数确定

现在，为了以更智能的方式实现此过程，已知使用先入先出（FIFO）队列这种数据结构非常有效。当然，即使不使用队列也可以解决这个问题。如果您对此不太了解，建议您使用自己想到的方法来解决。先入先出队列是具有以下功能的数据结构：

• 添加(Push): 在队列的末尾添加数据。
• 弹出(Pop): 移除队列的第一个数据。