Problem Statement

Squid loves painting vertices in graphs.

There is a simple undirected graph consisting of $N$ vertices numbered $1$ through $N$, and $M$ edges. Initially, all the vertices are painted in color $0$. The $i$-th edge bidirectionally connects two vertices $a_i$ and $b_i$. The length of every edge is $1$.

Squid performed $Q$ operations on this graph. In the $i$-th operation, he repaints all the vertices within a distance of $d_i$ from vertex $v_i$, in color $c_i$.

Find the color of each vertex after the $Q$ operations.

Constraints

• $1 ≤ N,M,Q ≤ 10^5$
• $1 ≤ a_i,b_i,v_i ≤ N$
• $a_i ≠ b_i$
• $0 ≤ d_i ≤ 10$
• $1 ≤ c_i ≤10^5$
• $d_i$ and $c_i$ are all integers.
• There are no self-loops or multiple edges in the given graph.

Partial Score

• $200$ points will be awarded for passing the testset satisfying $1 ≤ N,M,Q ≤ 2{,}000$.

Input

Input is given from Standard Input in the following format:

$N$ $M$ $a_1$ $b_1$ $:$ $a_{M}$ $b_{M}$ $Q$ $v_1$ $d_1$ $c_1$ $:$ $v_{Q}$ $d_{Q}$ $c_{Q}$

Output

Print the answer in $N$ lines. In the $i$-th line, print the color of vertex $i$ after the $Q$ operations.

Sample Input 1

7 7
1 2
1 3
1 4
4 5
5 6
5 7
2 3
2
6 1 1
1 2 2

Sample Output 1

2
2
2
2
2
1
0

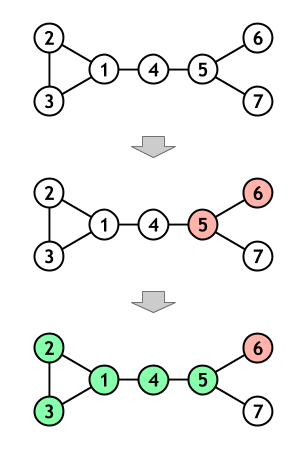
Initially, each vertex is painted in color $0$. In the first operation, vertices $5$ and $6$ are repainted in color $1$. In the second operation, vertices $1$, $2$, $3$, $4$ and $5$ are repainted in color $2$.

Sample Input 2

14 10
1 4
5 7
7 11
4 10
14 7
14 3
6 14
8 11
5 13
8 3
8
8 6 2
9 7 85
6 9 3
6 7 5
10 3 1
12 9 4
9 6 6
8 2 3

Sample Output 2

1
0
3
1
5
5
3
3
6
1
3
4
5
3

The given graph may not be connected.